希尔排序(Shell)
希尔排序
| 平均事件复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 稳定性 | 排序方式 |
|---|---|---|---|---|---|
| $O(nlogn)$ | $O(nlog^2 n)$ | $O(nlog^2 n)$ | $O(1)$ | 不稳定 | In-place |
简介
希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。
提算法贡献者:D.L.Shell
提出时间:1959 年
算法思想
特点
基于插入排序
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
使用增量序列来排序(Gap sequences)
希尔排序的好坏与增量序列的选择有关。
希尔排序中比较著名的增量序列有:
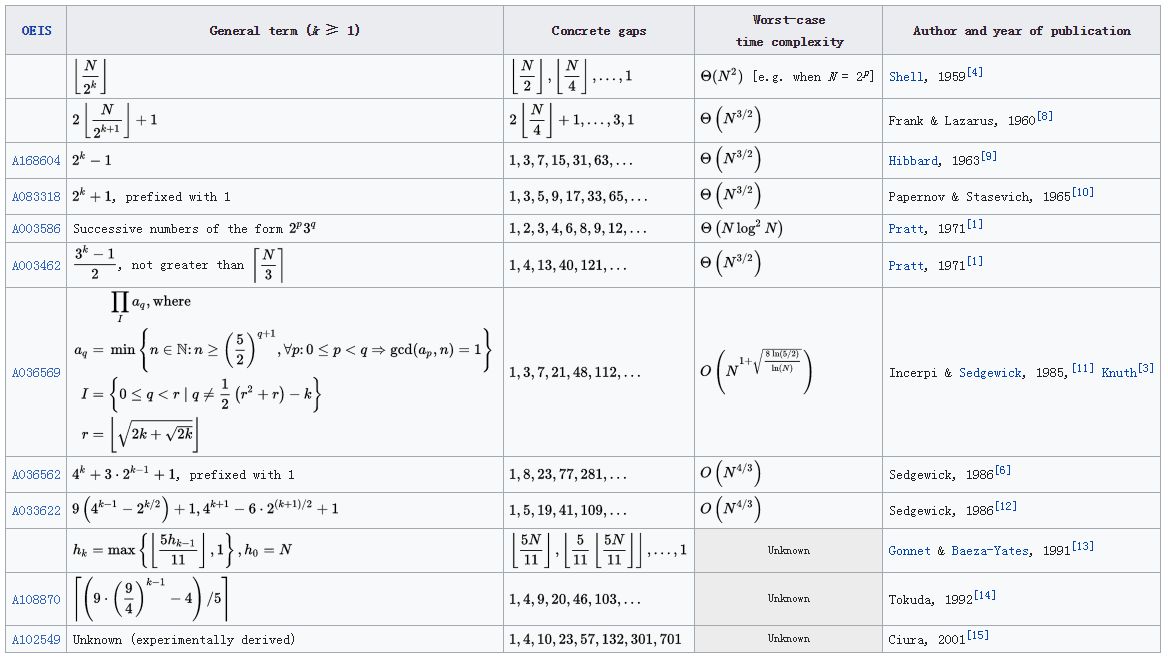
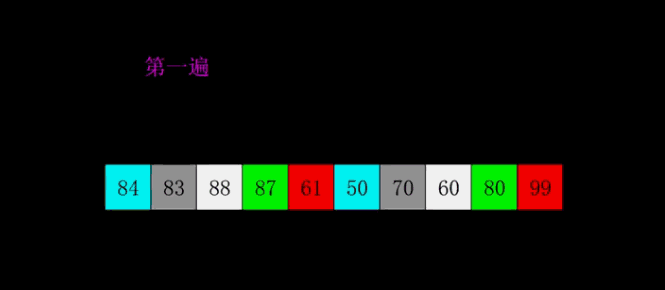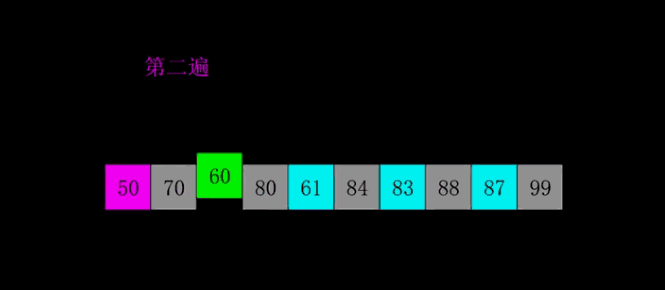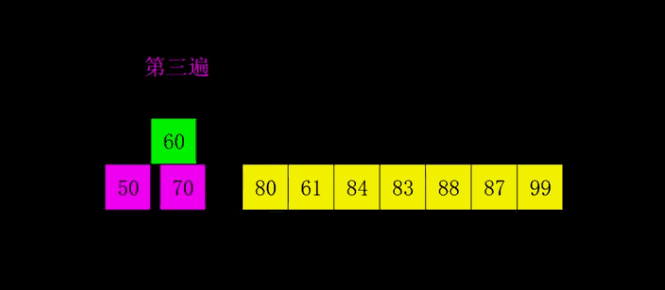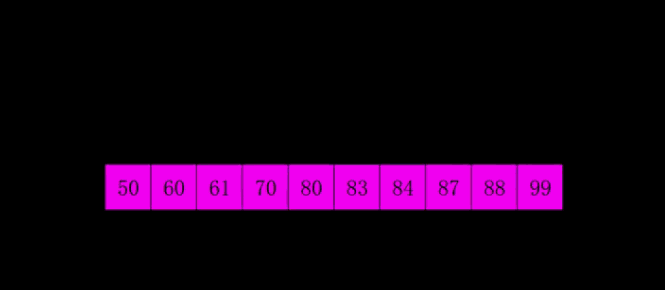
排序动画
动图展示的是增量序列为:5,2,1

代码设计
确定增量序列
选取一个合适的增量序列,假设序列为gaps[]。(注意增量序列需要倒序处理,确保最后一个是1)
外层遍历增量序列
每次选取增量序列中的一个序列来进行排序
1 | // foreach gaps[] |
内层进行跨增量的插入排序
首先从增量对应的数组下标开始,确定待排序数据范围
1 | // 循环次数是数组长度减去当前增量值 |
然后在待排序数据范围循环内部,根据某个增量跨度,将增量跨度的元素进行排序
1 | // 进行跨增量插排,比较当前下标的数据(array[j])和下标减掉增量的数据(array[j - gap])是否符合条件 |
将所有代码拼起来就是:
1 | public void shell(Comparable[] array, int[] gaps){ |
当然上面的代码是shell排序的通用模板,实际上写方法不唯一,如对于A003462增量序列,可以参考下面的代码:
1 | // 序列:121,40,13,4,1 |
排序实例
首先确定跨度,实例采用的跨度是h=3, 2,1,先使用3的跨度,定位到相应的元素

由于当前跨度是3,因此当前定位需要比较的元素为:
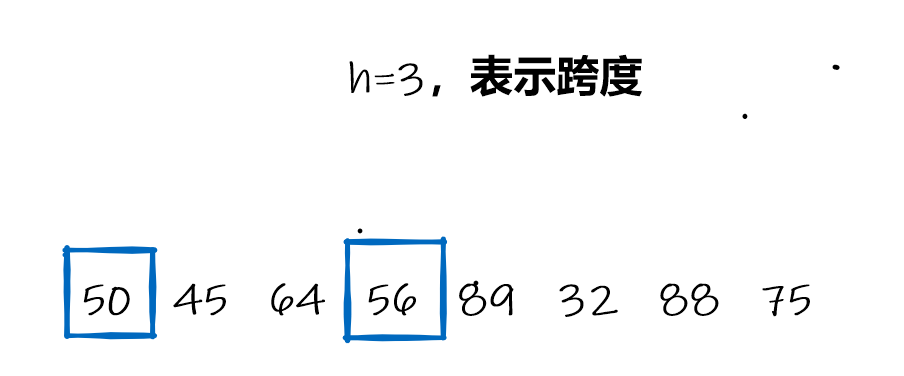
当前比较符合要求,定位下走一位:
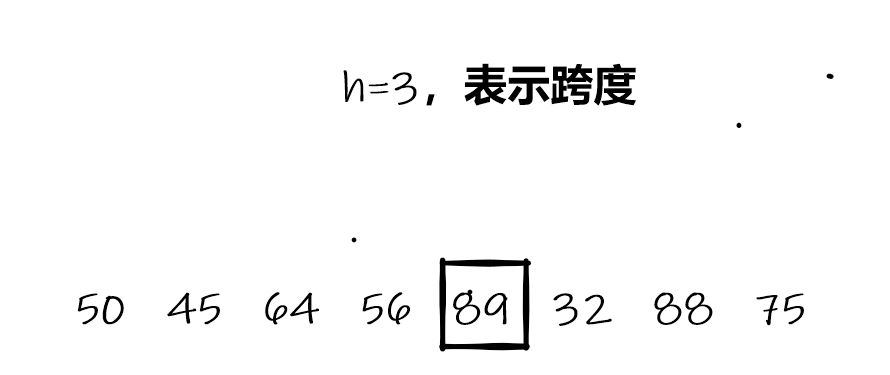
当下走到32时,出现比较交换
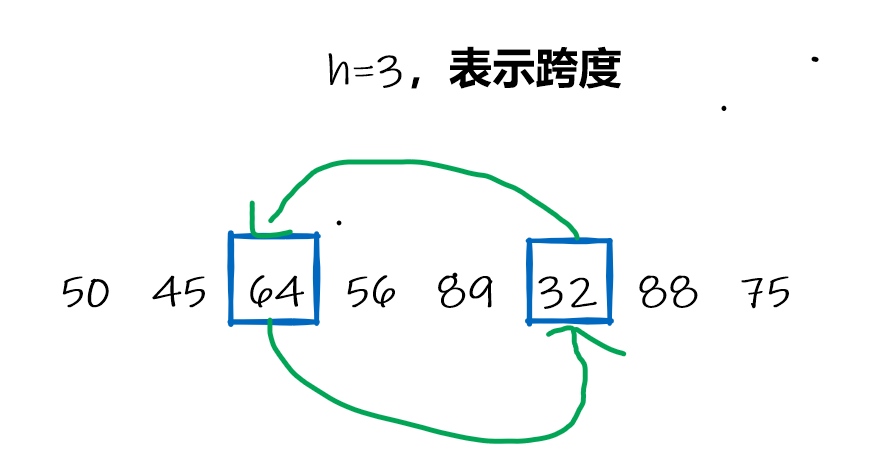
当走到88时,要进行插入比较定位的元素就是
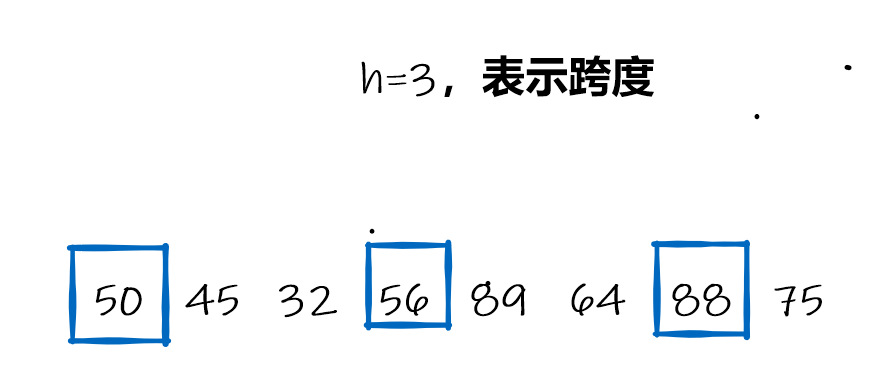
当h=3时,定位到75并处理好之后,一趟结束下来,序列应该变成这样:

调整跨度h = 2,定位从32开始

重复上面的步骤,h=2的最终序列就是:

最后调整h=1,最终排列的结果就是:
