插入排序（Insertion）

发表于 分类于 Changyan：

插入排序

插入排序

排序算法 平均事件复杂度 最好情况 最坏情况 空间复杂度 稳定性 排序方式
插入排序 $O(n^2)$ $O(n)$ $O(n^2)$ $O(1)$ 稳定 In-place

简介

插入排序，一般也被称为直接插入排序。对于少量元素的排序，它是一个有效的算法。

插入排序实际上会在数组中形成两个子数组，一个为待排序的子数组，一个为已经有序的子数组，因此，如果一个数组本身就是部分有序的，插入排序也会是一个选择。

算法本身采用减治法思想。

算法思想与设计

排序动画

插入排序

代码设计

首先插入排序讲整个大数组分成了两个关键子数组：

  • 已有序的数据
  • 待排序的数据

插入排序的目标数组一定包含这两部分，剩余的便是如何讲待排序的数据插入到已有序的数据中

因此编写插入排序代码的第一步便是确定待排序数据的规模，已确定外层排序顺序

1
2
3
4
5
// 从1开始是因为第一个元素单独构成了一个已有序的数据
// 剩下的从1开始的元素规划为待排序的数据
for(int i = 1; i < array.length; i++){
	
}

然后在待排序的数据中选出一个数据

1
Comparable target = array[i];

最后将target跟已有序的数据进行逐一比较确认位置下标j

1
2
3
4
// 在已有序的数据中寻找符合的位置，如果target比当前位置（array[j-1]）要小，则将当前位置的数据往后移
for(int j = i; j > 0 && less(target, array[j-1]); j--){
	array[j] = array[j-1];
}

这里对边界值进行解释，首先目标数据是跟前一个数相比，因此当target和 array[0]比较的时候（less函数），j为1也只能为1，换句话说j最小的情况是1，这也是为什么使用j>0条件的原因，当j等于1的时候条件仍然成立，这个时候就是：

1
array[1] = array[0];

当target比array[1-1]还要小的时候，则将有序数组下标为0的元素挪到下标为1的地方。这个时候下标为0的地方就空出来了。然后执行j--，j就等于0，不合条件，退出循环。也就是说目标数据的待插入位置为0。

同样当执行less(target, array[j-1])，注意当前array[j]为空位，跟前一个数比较的时候，less函数出现false，那么就确定array[j-1]要小于target，也就说明了插入位置为j。

因此我们最后一步便是让array[j] = target

1
array[i] = target;

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
for (int i = 1; i < a.length; i++) {
	// 临时存储要插入的值
    Comparable tmp = a[i];
    int j;
    // less():判断a[i]是否小于a[j - 1]
    for ( j = i; j > 0 && less(a[i], a[j - 1]) ; j--) {
    	// 如果a[i]小于a[j - 1]，则将a[j - 1]右移
        a[j] = a[j - 1];
    }
    // 知道找到比a[i]小的数，那么这时候的j-1就是这个小数的下标，j就是它的前一位，也就是目标位，替换
    a[j] = tmp;
}

实例

首先将第一个元素初始化为一个有序组，然后光标移向第二个有元素

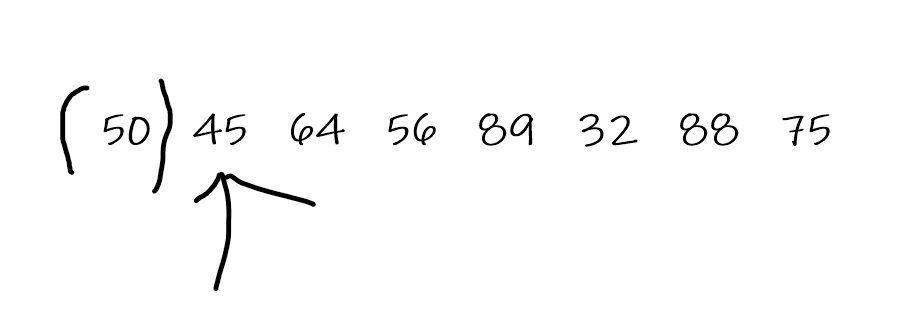
image-20210615221128408

然后将第二个元素进行定位

image-20210615221502845

形成：

image-20210615221552079

然后选取第三个元素，定位并插入到括号里面

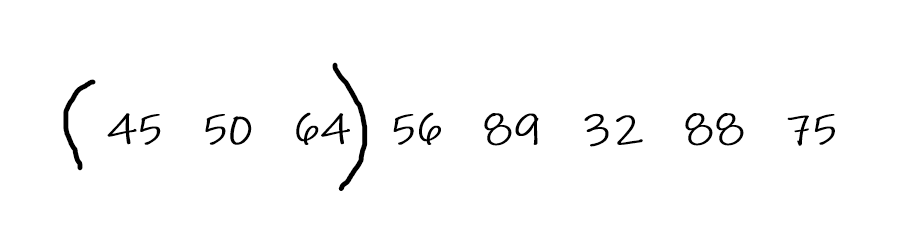
image-20210615221651930

然后选取第四个元素，重复定位并插入有序组里

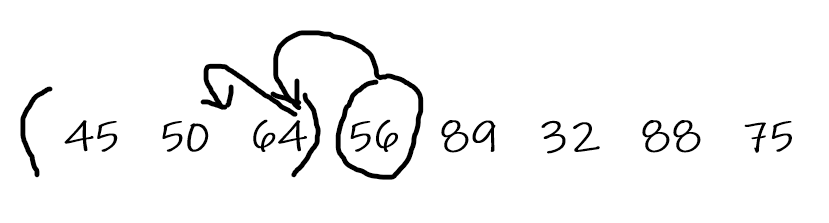
image-20210615221823595

重复上面的步骤，最终得到的就是有序数组

算法分析

最好情况

最坏情况

空间复杂度